RevisionDojo

Question 1

SLPaper 2

A local bakery offers fresh baguettes for delivery. The total cost to the customer, $C$ in Euros (€), is modeled by $C(n) = 3.2n + 5$ , where $n$ is the number of baguettes ordered and includes a fixed delivery fee.

1.

State what the value of $3.2$ represents.

[1]

2.

State what the value of $5$ represents.

[1]

3.

Write down the minimum number of baguettes that can be ordered.

[1]

4.

Sophie has 30 Euros. Find the maximum number of baguettes Sophie can order.

[3]

Question 2

HLPaper 1

The ticket prices for a concert are shown in the following table.

Ticket Type	Price (in Australian dollars, $)
Adult	15
Child	10
Student	12

The total amount of money from ticket sales was $7816.
There were twice as many adult tickets sold as child tickets. Let the number of adult tickets sold be x, the number of child tickets sold be y, and the number of student tickets sold be z.

1.

Write down three equations that express the information given above.

[3]

2.

Find the number of each type of ticket sold.

[2]

Question 3

SLPaper 2

Linda owns a field, represented by the shaded region R. The plan view of the field is shown in the following diagram, where both axes represent distance and are measured in metres. 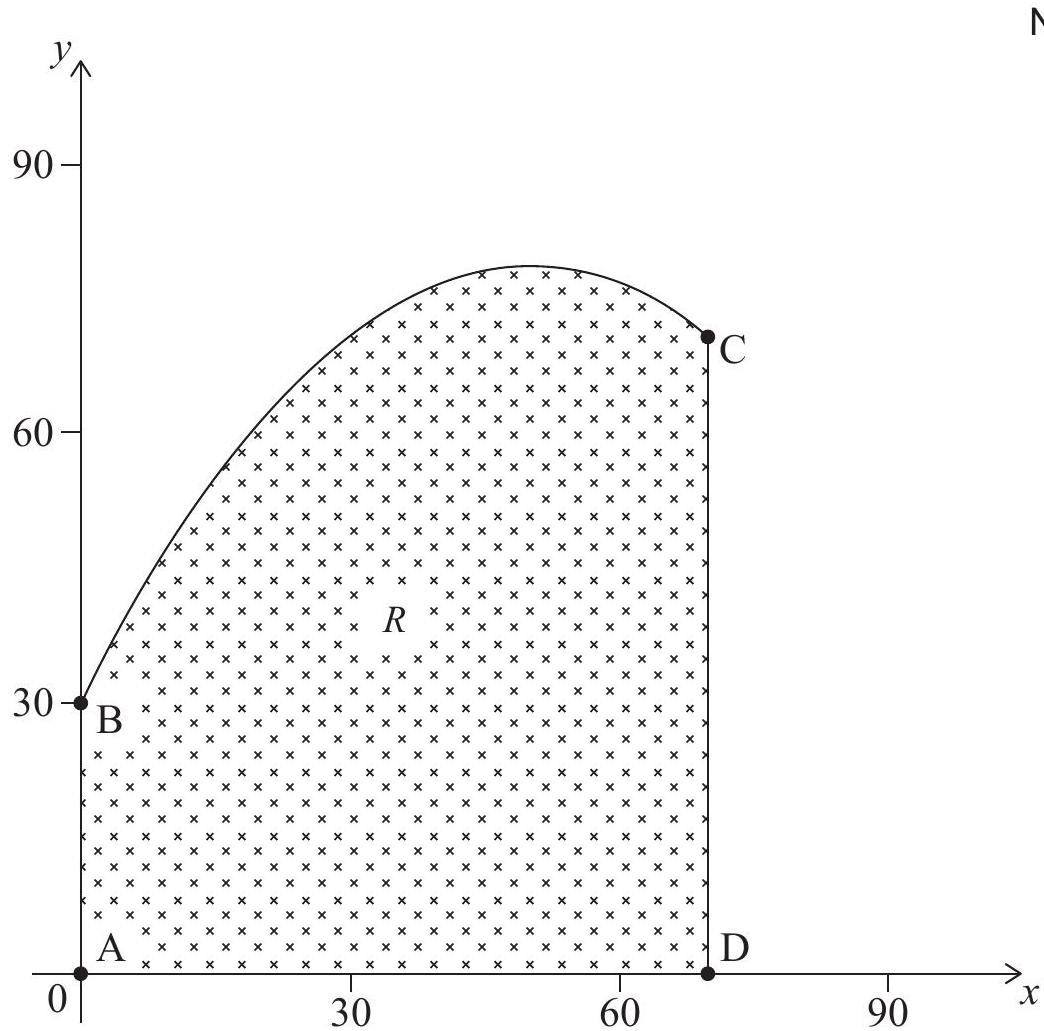The segments [AB], [CD] and [AD] respectively represent the western, eastern and southern boundaries of the field. The function, f(x), models the northern boundary of the field between points B and C and is given by f(x) = -x^2/50 + 2x + 30, for 0 ≤ x ≤ 70

1.

Find f'(x).

[1]

2.

Hence find the coordinates of the point on the field that is furthest north.

[5]

3.

Write down the integral which can be used to find the area of the shaded region R.

[1]

4.

Find the area of Linda's field.

[4]

5.

Calculate the percentage error in Linda's estimate.

[1]

6.

Suggest how Linda might be able to reduce the error whilst still using the trapezoidal rule.

[3]

7.

Find the x-coordinate of point E for the largest area of the square foundation of building EFGH.

[1]

8.

Find the largest area of the foundation.

[5]

Question 4

SLPaper 1

Olava’s Pizza Company supplies and delivers large cheese pizzas.

The total cost to the customer, $C$ , in Papua New Guinean Kina ( $PGK$ ), is modelled bythe function

$C (n) = 34.50 n + 8.50, n \geq 2, n \in ℤ,$

where $n$ , is the number of large cheese pizzas ordered. This total cost includes a fixedcost for delivery.

1.

State, in the context of the question,what the value of $34.50$ represents.

[1]

2.

State, in the context of the question,what the value of $8.50$ represents.

[1]

3.

Write down the minimum number of pizzas that can be ordered.

[1]

4.

Kaelani has $450 PGK$ .

Find the maximum number of large cheese pizzas that Kaelani can order fromOlava’s Pizza Company.

[3]

Question 5

SLPaper 2

In memory of the legendary musician Alex Star, tribute concerts continue to attract fans worldwide, decades after his passing in 1985. The number of attendees at these concerts, ${N(t)}$ , can be modeled by

${N(t) = 200 \cdot 1.28^t}$

where ${t}$ is the number of years since 1985.

1.

Calculate the time taken for the number of attendees to reach 100,000.

The number of attendees at a festival can be modelled by the function:

A(t) = \frac{200,000}{1 + e^{-0.4(t-10)}}

where $A(t)$ is the number of attendees and $t$ is the time in hours since the festival opened.

[2]

2.

Write down the number of attendees in the year 1985

[2]

3.

Calculate the number of attendees when ${t = 50}$

[2]

4.

If the global population in 2060 is projected to be 10 billion, explain why this model for the number of attendees might be unrealistic.

[3]

Question 6

HLPaper 1

Two schools are represented by points A(2,20) and B(14,24) on the graph below. A road, represented by the line R with equation -x+y=4, passes near the schools. An architect is asked to determine the location of a new bus stop on the road such that it is the same distance from the two schools.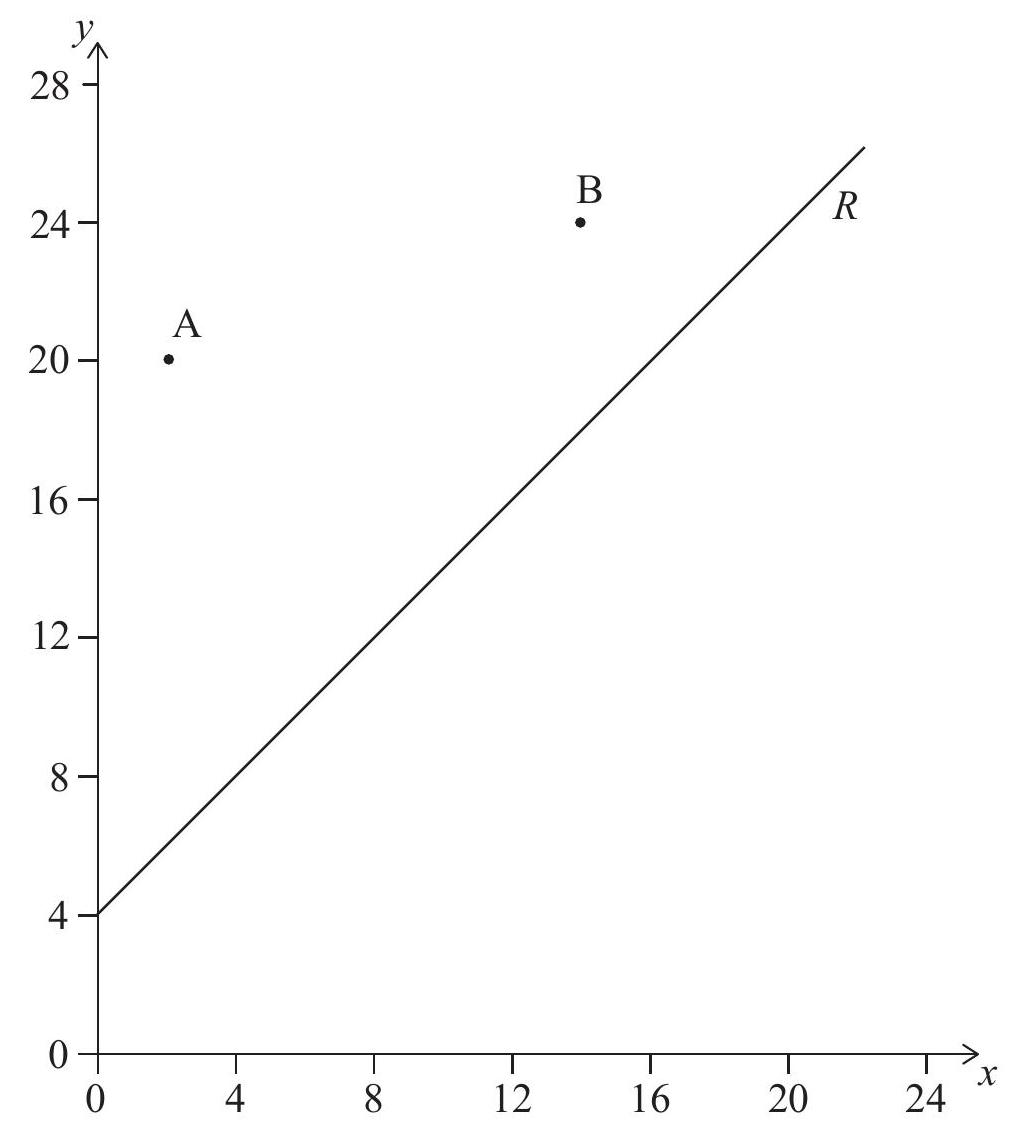

1.

Find the equation of the perpendicular bisector of [AB]. Give your equation in the form y=mx+c.

[5]

2.

Determine the coordinates of the point on R where the bus stop should be located.

[2]

Question 7

SLPaper 2

A biologist studies a bacteria population, modeled by $P(t) = 15 \cdot 2^{0.6t}$ , where $t$ is in hours.

1.

Find the initial population if:

The population after 3 years is 1331
The growth rate is 10% per year
The population grows exponentially

[2]

2.

Calculate the population after 5 hours.

[2]

3.

If the petri dish has a capacity of 10,000 bacteria, find the time to reach this capacity.

Given the logistic equation:

P(t) = \frac{10000}{1 + 9e^{-0.7t}}

where $P(t)$ represents the population at time $t$ .

Find the time $t$ when $P(t) = 10000$ .

[3]

Question 8

SLPaper 1

In an experiment, a number of fruit flies are placed in a container. The population of fruit flies, P , increases and can be modelled by the function

$P\left( t \right) = 12 \times {3^{0.498t}},\,\,t \geqslant 0,$

where t is the number of days since the fruit flies were placed in the container.

1.

Find the number of fruit flieswhich were placed in the container.

[2]

2.

Find the number of fruit fliesthat are in the container after 6 days.

[2]

3.

The maximum capacity of the container is 8000 fruit flies.

Find the number of days until the container reaches its maximum capacity.

[2]

Question 9

SLPaper 2

The temperature ${T(t)}$ of a hot beverage cools over time ${t}$ (in minutes), modeled by

${T(t) = T_{env} + (T_0 - T_{env}) e^{-kt}}$

where ${T_{env} = 20^\circ C}$ , ${T_0 = 90^\circ C}$ , and ${T(10) = 50^\circ C}$ .

1.

Determine ${k}$

[3]

2.

Predict the temperature after 30 minutes.

[2]

3.

Describe what the decay constant ${k}$ tells us about the cooling rate.

[2]

Question 10

SLPaper 1

A factory produces engraved gold disks. The cost $C$ of the disks is directly proportional to thecube of the radius $r$ of the disk.

A disk with a radius of $0.8$ cm costs $375$ US dollars (USD).

1.

Find an equation which links $C$ and $r$ .

[3]

2.

Find, to the nearest USD, the cost of disk that has a radius of $1.1$ cm.

[2]

Number and Algebra15 subtopics

Functions10 subtopics

Geometry and Trigonometry16 subtopics

Statistics and Probability19 subtopics

Calculus18 subtopics

Internal Assessment (IA)3 subtopics

SL 2.6—Modelling skills